KVS Tutorial (version 2〜)

kvs version 3.0

kvs : https://github.com/naohisas/KVS

インストール

基本的な使い方

伝達関数を調整する

KVSプログラムの作成

3次元ベクトルの演算

行列クラス

行列の演算（行列クラスの応用）

乱数生成

オブジェクトについて

構造型ボリュームデータの作成

面データの可視化

等値面の可視化

可視化パイプライン

レイキャスティングの実装

PBVRの実装

付録：プログラム集　

点群データの可視化

PLYデータ（点群データ）

点群の可視化

確率的ポイントレンダリング

例　SPBRの実装

問題　不透明度の変更

確率的ポイントレンダリング

ここでは，点群データの半透明可視化手法である「確率的ポイントレンダリング（Stochastic Point-based Rendering; SPBR) 」を用いて点群データの可視化を行っていく．

（SPBRの詳細は参考文献：

Satoshi Tanaka, Kyoko Hasegawa, Yoshiyuki Shimokubo, Tomonori Kaneko,Takuma Kawamura, Susumu Nakata, Saori Ojima, Naohisa Sakamoto, Hiromi T. Tanaka, and Koji Koyamada,
“Particle-Based Transparent Rendering of Implicit Surfaces and its Application to Fused Visualization”,
EuroVis 2012, pp.25–29 (short paper), Vienna

※SPBRは PBVRをボリュームデータからサーフェスデータへ拡張した手法であり，

• ＊　点の生成，
• ＊　点の投影，
• ＊　画像のアンサンブル平均（平均回数をリピートレベルとよぶ），
• ＊　半透明画像を生成，

は同様の手順である．

SPBRでは曲面上に点が一様に存在すると仮定すると，点密度（点数 n ）と不透明度 α に以下のような関係式が定義できる（詳細は上述の論文を参考）．

ただし．s_p は点の断面積，s_Aは曲面全体の面積，L はリピートレベルを表す．

つまり，SPBRでは可視化結果の不透明度は，

・点数

・リピートレベル

に依存する．

ただし，一般的に点の可視化（ポイントレンダリング）は1ピクセル相当の点で描画するため，スクリーンの解像度にも不透明度が依存してしまう．

ここではスクリーンの解像度（点の断面積 s_p）について，説明する．

下の様な球を20×20の解像度のスクリーンに原点を中心とした半径1の球を投影する事を考える．

ここで，点の断面積 s_p とは「スクリーン座標系における1ピクセルを世界座標系に逆変換したときの大きさ」である．

上の図の例でいえば，半径1の球を20×20の解像度のスクリーンに投影したときに，1ピクセルを球と同じ座標系に変換したらいくつになるか？を考えれば良い．

つまり，球は幅が 2 で，スクリーンは幅 20 ピクセルなので，この例の場合には，

1ピクセルの幅 = 2/20 = 0.1 となる．

別の例として，スクリーンの解像度が 512 × 512 になれば

1ピクセルの幅 = 2/512 = 0.00390625 となり，ピクセルの幅が小さくなることが分かる．

つまり，スクリーンの解像度によって s_p の値が変化する．

今，簡単のために縦横のサイズが同じ球を例に見ているが，実際は縦横のうち大きい方に合わせる（画面からオブジェクトがはみ出さないように投影する）．

例　SPBRの実装　〜球面上に一様サンプリング〜

実際に，半径1の球に点を生成するプログラムを作って，SPBRで半透明可視化を行うプログラムを作成していこう．

ここでは，不透明度とリピートレベル，スクリーンの解像度を入力パラメタとして設定し，球面上にサンプリングする点数を計算する．

1.　作業ディレクトリの作成

作業ディレクトリに「spbr」というディレクトリを作成して，移動して下さい．

$ mkdir  SPBR

$ cd SPBR

2.　main.ccp の作成

「main.cpp」というファイルを作成して下さい．

このプログラム例では，不透明度を 0.2, リピートレベルを 50, スクリーンの解像度を 512 とし，また球の半径は 1.0 で作成した点の色をシアン ( 0, 255, 255 ) と固定することとする．これらを固定パラメタとして，最初に書いておくこととする．

int main( int argc, char** argv )
{
  const double ALPHA = 0.2;      // 不透明度
  const int REPEAT_LEVEL = 50;   // リピートレベル
  const int IMAGE_RESOLUTION = 512;  // スクリーンの解像度

  const unsigned char  POINT_COLOR[3] = { 0, 255, 255 }; // 点の色（シアン）
  const double RAD = 1.0;    // 球の半径 
  //---- ここから下にプログラムを追記していく

  } 

3.　生成点数の計算

設定したパラメタから，球面上に生成するのに必要な点数を計算する，ここでは，簡単のため球がスクリーンいっぱいに投影すると仮定して点の断面積を求める．

（ただし，KVSではオブジェクトがはみ出さないようにマージンが設定されており，正確には

　　 kvs::detail::CalculateSubpixelLength( ) 関数を通して点の断面積を取得する方が理想的である）

また，点数の計算は double型で行った後に，整数型にキャストする．

  double diameter = 2.0 * RAD;    // 球の直径
  // ピクセルの幅を球の幅とスクリーンの解像度から概算
  double pixel_width = diameter / (double)IMAGE_RESOLUTION;  

  double pixel_area = pixel_width * pixel_width;    // 点の断面積
  double area = 4.0 * M_PI * RAD * RAD;                 // 球の表面積

  // 定義式から球面上に必要な点の数を計算する
  double nall =
   ( log(1.0 - ALPHA) / log(1.0 - pixel_area/area) * (double)REPEAT_LEVEL );
  size_t numVert = (size_t)nall;   // 整数型にキャスト

4.　球面上に一様な点をサンプリングする

numVert 個の点を球面状にサンプリングすることを考えよう．

簡単には，球を極座標で考え，

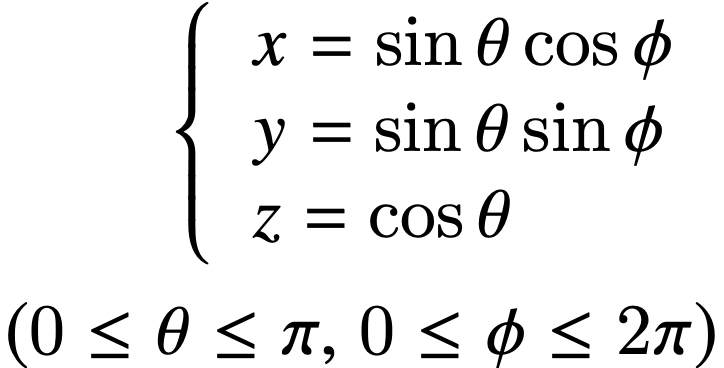
θとφを乱数で生成して点を生成する方法が考えられる．但し．この場合には，z の値が±1 の付近（地球でいう北極・南極の辺り）で点密度が高くなってしまい，SPBRでの曲面上で一様であるという仮定に従わない．

そこで，z の値が [-1, 1] で一様になるように考える， より， を代入して新たに [0, 1]で一様な乱数を s, t とすれば，上の式は，

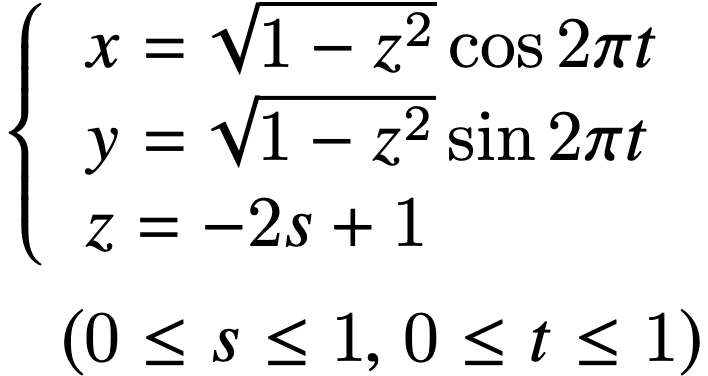
で書き表すことができる．

※球の半径を変更したい場合は，x, y, zそれぞれに半径 r をかければよい．

ここで，s, t は乱数の生成で用いた一様乱数 kvs::MersenneTwister を用いる．

また，球面上の法線は球を とすれば，法線は （法線ベクトルは正規化する）で求めることができる，

  std::vector <kvs::Real32> coords;    // 全点の位置情報を格納
  std::vector <kvs::Real32> normals;   // 全点の法線情報を格納
  std::vector <kvs::UInt8>  colors;    // 全点の色情報を格納

  kvs::MersenneTwister uniRand;   // 一様乱数 s, t 
  for( size_t i = 0; i < numVert; i++ ) {  // numVert 個の点をランダムに生成する
    //--- 球面上に一様な点を生成する 
    double z = RAD * ( -2.0 * uniRand() + 1.0); // ここでのuniRand() は上式の s
    double sinTheta = sqrt( 1.0 - z * z );
    double phi = 2.0 * M_PI * uniRand();     // ここでのuniRand() は上式の t
    double x = RAD * sinTheta * cos( phi );
    double y = RAD * sinTheta * sin( phi );
    // ランダムに生成した位置座標を格納
    coords.push_back( (float)x );
    coords.push_back( (float)y );
    coords.push_back( (float)z );
    // 法線を計算して，登録する
    kvs::Vector3f norm( (float)x, (float)y, (float)z );
    norm.normalize( );   // 正規化を行う
    normals.push_back( norm.x() );
    normals.push_back( norm.y() );
    normals.push_back( norm.z() );
    // 色を登録する（ここでは全ての点は同じ色とする）
    colors.push_back( POINT_COLOR[0] );
    colors.push_back( POINT_COLOR[1] );
    colors.push_back( POINT_COLOR[2] );
  }  

5.　PointObjectの生成

生成した点の情報から，kvs::PointObject のインスタンスを作成する．

  kvs::PointObject *point = new kvs::PointObject();
  point->setCoords( kvs::ValueArray<kvs::Real32>( coords ));    // 位置情報
  point->setNormals( kvs::ValueArray<kvs::Real32>(normals ) );  // 法線情報
  point->setColors( kvs::ValueArray<kvs::UInt8>( colors ) );    // 色情報
  point->updateMinMaxCoords();     // 登録した点群の位置情報の最大値・最小値を求める
  point->print( std::cout );       // 生成したPointObjectの情報を標準出力  

6.　Renderer の生成　

SPBRではPBVRと同様にkvs::glsl::ParticleBasedRenderer を使い，リピートレベルを設定する．

また，SPBRでは不透明度が1ピクセルの大きさによることから，ここでは，KVSの標準機能である粒子拡大（点がカメラからの距離に応じて拡大されて提示される）を無効にする．

  kvs::glsl::ParticleBasedRenderer* renderer =
    new kvs::glsl::ParticleBasedRenderer();
  renderer->setRepetitionLevel ( REPEAT_LEVEL );   // リピートレベルの設定
  renderer->disableZooming();    // 粒子拡大を無効化 

7．描画

描画についてはこれまでと同様に，kvs::Application と kvs::Screen を使う．

Screenの解像度が変わってしまうと，描画結果として不透明度が変わってしまうため，点数の計算に使った解像度を設定する．また，半透明描画を行うため，背景色を黒にすることで，可視化結果への背景色の影響を無視することにする．

最後に，ScreenにPointObjectとParticleBasedRendererを登録して描画する．

  kvs::glut::Application app( argc, argv );
  kvs::glut::Screen screen( &app );
  //  Screeの解像度を設定
  screen.setGeometry( 0, 0, IMAGE_RESOLUTION, IMAGE_RESOLUTION ); 
  //  背景色を黒に設定
  screen.setBackgroundColor( kvs::RGBColor ( 0, 0, 0 ) );
  screen.setTitle( "SPBR" );
  screen.registerObject( point, renderer );
  screen.show();

  return( app.run() );

8.　ヘッダファイル

使用したKVSクラスをインクルードします．ここでは，

• kvs::MersenneTwister
• kvs::PointObject
• kvs::glsl::ParticleBasedRenderer
• kvs::glut::Application
• kvs::glut::Screen

を使用したので以下をインクルードする．

#include <kvs/MersenneTwister>
#include <kvs/PointObject>
#include <kvs/ParticleBasedRenderer>
#include <kvs/glut/Application>
#include <kvs/glut/Screen>

9.　まとめ

以上をまとめたプログラムはこちら：　SPBR.zip

10.　コンパイルと実行

作成したプログラムをコンパイル，実行しよう．

KVSプログラムをコンパイルするためにはkvsmakeコマンドを用いてMakefileを作成した後に．コンパイルを行う．

$ kvsmake -G　　　　　　　　　　<-- Makefile の作成

$ kvsmake　　　　　　　　　　　　<-- コンパイル

エラーなくコンパイルできたら，実行してみよう．

$ ./SPBR　

以上を実行すると，半透明なシアン色の球が描画できる．

問題　不透明度を変更してみよう

上の例では不透明度を 0.2 で固定していたので，標準入力から不透明度を入力できるようにプログラムを変更し，点数がどのように変わるか調査せよ．

また，不透明度は 0 より大きく，1より小さい値 ( 0 < α < 1 ) になるようにエラー処理を行うこと，

※あまり1に近い値を入力すると点数が膨大になるため， 0.99 程度で止めておくのが現実的である．

応用　PLYデータをSPBRで可視化してみよう

前のページのPLYデータの読み込みとこのページのSPBRレンダラの設定の部分を合わせて，PLYデータを読み込んで半透明可視化を行うプログラムを完成させよ．

また，PLYデータ（計測データ）はこのページのように曲面上に点を生成することが困難である．

計測データの半透明可視化をどのように実現しているか調査せよ．

Modefied at April 10, 2023

TOP