KVS Programming Guide

乱数クラスについて

KVSには乱数生成のためのクラスとして

一様乱数：MersenneTwister

正規乱数：BoxMuller

の2つの乱数のクラスがあります．

これらの乱数クラスには，乱数値を戻り値にするほか，種を設定したり，分布を変更したりすることができます．

ここでは，乱数クラスのもつメソッドについて説明したあと，円周率をモンテカルロ法で求めるプログラムを作成します．

同時に平均と標準偏差も求めてみましょう．

乱数クラスのメソッド

乱数クラスには，乱数値を戻り値にするほか，種を設定したり，分布を変更したりすることができます．

詳しくはソースコード

　(KVSのソースをダウンロードしたディレクトリ) kvs-src/Source/Core/Numeric/MersenneTwister.h

　(KVSのソースをダウンロードしたディレクトリ) kvs-src/Source/Core/Numeric/BoxMuller.h

を見てみて下さい．ここでは，各メソッドについて使い方を説明します．

コンストラクタ

乱数のコンストラクタとしては，次の2種類が用意されています．

// 引数なし
kvs::MersenneTwister uniRand;	// 一様乱数
kvs::BoxMuller normRand;	// 正規乱数
// 乱数シードを設定する
kvs::MersenneTwister uniRand2( 261422 );	// 一様乱数
kvs::BoxMuller normRand2( 261422 );		// 正規乱数

乱数を生成する

乱数を生成するためには operator () を用います．

KVSでは標準で

一様乱数　：　[0, 1] の区間の一様乱数
正規乱数　：　N(0, 1 ) の正規分布をもつ正規乱数

を生成します．

std::cout << "[0, 1] : 一様乱数 " << uniRand() << std::endl;
std::cout << "N(0, 1) : 正規乱数 " << normRand() << std::endl;

std::cout << "[0, 1] : 一様乱数 " << uniRand2() << std::endl;
std::cout << "N(0, 1) : 正規乱数 " << normRand2() << std::endl;

乱数の分布を変更する

一様乱数で区間 [0, n] となるように値を返すには：

　　rand( const double n )

正規分布の N( mu, sigma2 ) に従った乱数の値を返すには：

　　rand( const double mu, const double sigma2 )

　　aただし，mu; 平均，sigma2 ：分散

とします．

// 乱数の分布を変更する
std::cout << "[0, 100] : 一様乱数 " << uniRand.rand( 100 ) << std::endl;
std::cout << "N(2, 10) : 正規乱数 " << normRand.rand(2, 10) << std::endl;

例　モンテカルロ法を使って円周率を求める

モンテカルロ法で面積を求めるには，紙の上に適当な図形を描いて紙の上に均等に砂粒をばらまき，砂粒が図形内に入った割合を紙全体の面積にかけます．これによりおおよその面積を求めることができます．

ここでは(半径１の円面積)/4 をモンテカルロ法で求めた後に4をかけて円周率を求めています．

円周率を求めるためには，[0, 1]×[0, 1]の矩形内に乱数を生成し，その中からx² + y² < 1 内に入る点を数えます．

1.　作業ディレクトリの作成

作業ディレクトリに「CreateRandom」というディレクトリを作成して，移動して下さい．

$ mkdir CreateRandom
$ cd CreateRandom

2.　main.ccp の作成

「main.cpp」というファイルを作成して下さい．

一様乱数を生成するために，kvs::MersenneTwister クラスのインスタンスを生成します．

また，ここでは試行回数を1000回とします．

int main( void )
{
   kvs::MersenneTwister uniRand;	// 一様乱数
   kvs::BoxMuller normRand;	// 正規乱数
 
   // 乱数の試行回数
   const int trialNum = 1000;
 
   return ( 0 );
}

3.　初期値の設定

x² + y² < 1 内に入る点の数を数えるための変数，および，平均と標準偏差を計算するための変数に0を代入します．

// 円内に発生した点の数を数える
int num = 0;
// 平均と標準偏差を求めるための初期値
double uniAve = 0.0, uniDp = 0.0;

4. 数を数える

点（x, y) として[0, 1] の乱数をそれぞれ生成し，x² + y² < 1 内に入る点の数を数える．

さらに，平均と標準偏差を求めるために和と２乗和を計算する．

for( int i=0; i<trialNum; i++ ) {
   // [0, 1] 内で乱数を生成
   double x = uniRand();
   double y = uniRand();
   // x*x + y*y < 1 内に生成された点の数を数える
   if( ( x*x + y*y ) < 1.0 )
      num++;
 
   // 和と2乗和を計算
   uniAve += x;
   uniDp += ( x * x );
}

5. 円周率を求める

生成した総数に対して x² + y² < 1 内に入った数の割合を調べて円周率を求める．

また，平均と標準偏差を求める（[0,1] の一様乱数の標準偏差は1/12 になることを確認してみよう）．

// 円周率を求める
double pi = (double)num/(double)trialNum * 4.0;
std::cout << num << " " << trialNum << std::endl;
std::cout << "円周率 : " << pi << std::endl;
 
// 平均と標準偏差を求める
uniAve /= (double)trialNum;
uniDp = uniDp/(double)trialNum - uniAve*uniAve;
std::cout << "-- 一様乱数 -- " << std::endl;
std::cout << "平均 : " << uniAve << " 標準偏差 : " << uniDp << std::endl;

6. ヘッダファイル

ここで使用したKVSクラスをインクルードします．ここでは，

kvs::MersenneTwister
kvs::BoxMuller

を使用しました．

#include <kvs/MersenneTwister>
#include <kvs/BoxMuller>

7.　まとめ

以上をまとめたプログラムはこちら：　CreateRandom.tgz

8.　コンパイルと実行

作成したプログラムをコンパイル，実行してみましょう．

KVSプログラムをコンパイルするためにはkvsmakeコマンドを用いてMakefileを作成すると簡単にコンパイルを行うことができます．

$ kvsmake -G　　　　　　　　　　<-- Makefile の作成

$ kvsmake　　　　　　　　　　　　<-- コンパイル

エラーなくコンパイルできたら，実行してみましょう．

以下のような実行結果が得られると思います．

$ ./CreateRandom　　　　　　　　　　　<-- Windows環境ではCreateRandom.exe となります
[0, 1] : 一様乱数 0.352003
N(0, 1) : 正規乱数 0.24365
[0, 1] : 一様乱数 0.606438
N(0, 1) : 正規乱数 -0.447015
[0, 100] : 一様乱数 66.4808
N(2, 10) : 正規乱数 -8.92791
円周率 : 3.08
-- 一様乱数 --
平均 : 0.482417 標準偏差 : 0.0840314

以上のように，KVSでは乱数列を扱うことができます．

問題　円上にランダムに点を生成し，plot してみよう

円上にランダムに点群を生成して，ファイルに出力し，その結果をGnuplot を使って可視化してみましょう．

円上に点を生成するためには媒介変数表示を使って

x = r cos( θ )

y = r sin( θ )

　（ただし，r は半径）

x, y 座標を決定します．

Gnuplot のインストール

1) Gnuplotのインストール

gnuplot のWebページ：http://www.gnuplot.info/
からダウンロードします．

Macの場合は，同Webページの「 contributed executables for OSX」
からgnuplot-5.0.5-quartz.pkgファイルをダウンロードします．
（2017年4月21日現在）

ダブルクリックしてインストールすれば，アプリケーションフォルダに「gnuplot」がインストールされます．

2) 結果の確認

ファイルに出力した点群をgnuplot で表示するには，gnuplot 上で

> set size square 　　　　<-- 表示画面を正方形にする

> plot "test.dat" with points pointtype 7 　　<-- ファイルから点群を読み込み●で描画

この結果は以下の通り．

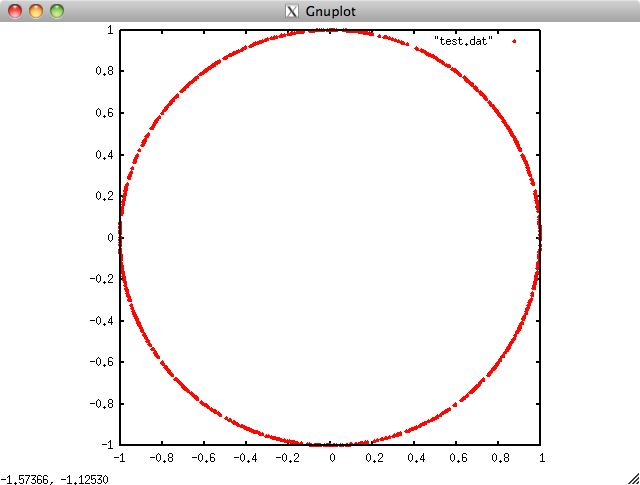
Result of PNUPLOT

Gnuplot による点群描画結果

Updated at July 4, 2014

at April 21, 2017

KVS Tutorial (version 2〜)